Задание 2. Решение — Убираем лишние скобки (дополнительный пункт 1) Swift 1.2 и Swift 2.0

Опубликовано автором

Текст Домашнего задания на английском языке доступен на  iTunes в пункте “Developing iOS 8 app: Programming: Project 2″.  Текст Домашнего задания на русском  языке доступен на

Задание 2 iOS 8_new.pdf

Результаты выполнения задания можно обсуждать на форуме Swift[ru] . Ваше решение может быть лучше и интереснее. Выкладывайте его в Github, давайте ссылку на Dropbox или используйте другие системы управления версиями. Xcode  работает напрямую с Github.

Пункт 1 дополнительный

Сделайте так, чтобы ваша description имела как можно меньше круглых скобок для бинарных операций.

Теоретическая часть согласно подсказке в Задании 2 потребует добавления концепции “приоритета (precedence) операций” в Op вашего CalculatorBrain. 

Заметим, что все нижеприведенные рассуждения касаются только перевода нашего стэка, записанного в форме обратной польской записи (RPN), не требующей применения скобок, в инфиксную форму со скобками. Инфиксная форма нужна только для представления описания стэка в привычной для пользователя форме var description и не влияет на вычисления нашего калькулятора.

Приоритет, ранг или старшинство операции или оператора согласно Wikipedia — формальное свойство оператора/операции, влияющее на очередность его выполнения в выражении с несколькими различными операторами при отсутствии явного (с помощью скобок) указания на порядок их вычисления. Например, операцию умножения обычно наделяют бо́льшим приоритетом, чем операцию сложения, поэтому в выражении  X + Y * Z  будет получено сначала произведение Y * Z  , а потом уже сумма.  Если порядок операций именно такой, то никаких скобок не требуется. Если нужен другой порядок операции, например сначала сумма  (X + Y), а потом произведение , то применяют круглые скобки  (X + Y) * Z.

У нас порядок операций строго определен стэком операндов и операций, который моделируется  перечислением enum Op. Поэтому, нам лишь приходится выбирать: ставить круглые скобки или нет, в зависимости от соотношения приоритетов между  приоритетом «родительской» операции (в нашем примере *) и  приоритетом операции для операнда (в нашем примере +). Если  приоритетом «родительской» операции выше приоритетом операции для операнда, то мы должны использовать круглые скобки, а в противном случае — нет. 

Операции могут иметь одинаковый приоритет, тогда они вычисляются по правилу ассоциативности, установленному для этих операций. Правило означает как будут выполняться операции в отсутствии скобок. Есть правая  и левая ассоциативность операции. Большинство привычных нам операций имеют левую ассоциативность. Это означает, что операции начинают выполняться слева направо. Например, для  операции сложения в выражении X-Y+Z  сначала будет вычисляться X-Y, а затем (X-Y) + Z. Если нам нужен другой порядок выполнения, то мы должны поставить круглые скобки. Например, в этом случае  X-(Y+Z). Однако если у нас  X+Y+Z, то результат не зависит от порядка группировки : (X+Y)+Z  и X+(Y+Z) дают одинаковый результат. В этом случае важно, обладает ли операция свойством коммутативность, то есть зависит ли результат вычисления от перемены мест операндов. Вычитание не является коммутаторной операцией и нам иногда придется поставить круглые скобки в случае одинаковых приоритетов. Сложение является коммутаторной операцией и нам никогда не придется ставить круглые скобки в случае одинаковых приоритетов. Такая же ситуация складывается с парой Умножение и Деление. Причем если операция не является коммутаторной — Вычитание и Деление — то окружать круглыми скобками нужно только операнд, стоящий справа. В нашем примере  X-(Y+Z) для операции Вычитание операнд (Y+Z) является правым операндом и должен быть окружен круглыми скобками. В случае   X — W — (Y+Z)  для центральной операции Вычитания операндами будут X — W и (Y+Z) , но только правый операнд (Y+Z) нуждается в круглых скобках.

Отвлекаясь в сторону, напомню, что операторы в Swift также имеют свойства  preference и associativity. Например,

infix operator ** { associativity left precedence 160 }

Наибольшее количество круглых скобок в нашем калькуляторе плодится в бинарных операциях, поэтому постараемся в первую очередь избавиться от них.
Добавляем две новые вычисляемые переменные в перечисление enum Op в нашем CalculatorBrain

var precedence: Int
 var commutative: Bool 

Для бинарных операций эти значения будут задаваться при определении операций, а для других вариантов перечисления enum Op будут возвращаться значения  по умолчанию: для precedence — максимальное целое значение Int.max, а для  commutative — true:

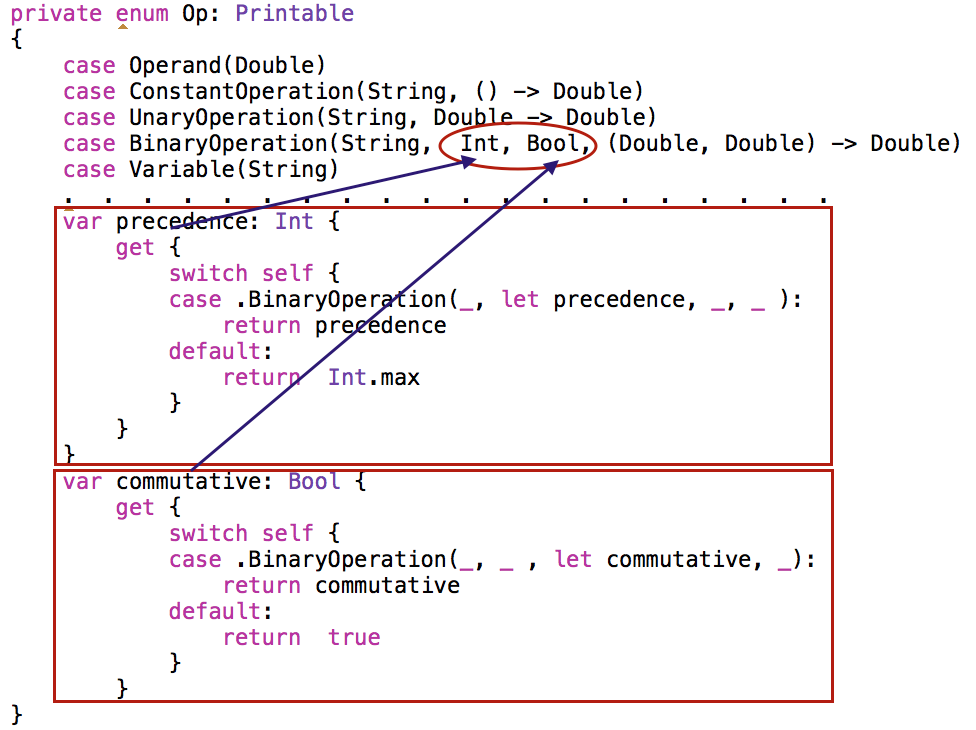
Screen Shot 2015-03-29 at 11.44.03 AM
Для операций умножения и деления устанавливаем precedence — 2, а для сложения и вычитания —1. Для всех операций, кроме  вычитания  и деления устанавливаем  commutative — true, а для вычитания  и деления — false.

Screen Shot 2015-03-29 at 11.50.57 AM
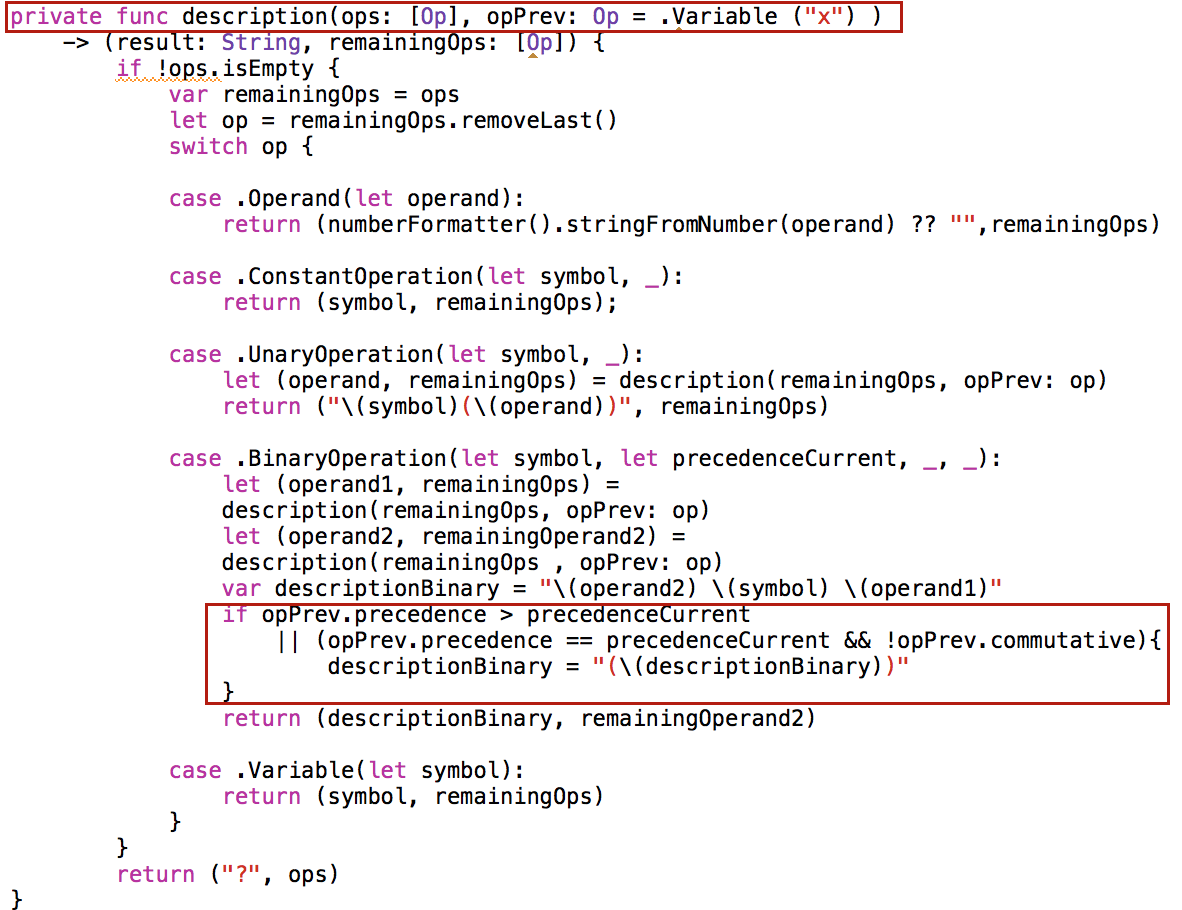
В возвращаемый кортеж вспомогательного рекурсивного метода  private description метода добавляем дополнительный параметр — приоритет (precedence) родительской операции precedence: Int. Бинарные операции проверяют свой текущий приоритет и сравнивают его с приоритетом операций аргументов. Если приоритет текущей операции выше приоритета операции аргумента, то мы заключаем соответствующий аргумент в круглые скобки. Если приоритет текущей операции равен приоритету операции аргумента, то мы анализируем коммутативность commutative текущей операции и в зависимости от этого, добавляем или нет круглые скобки. Второй операнд operand2, который затем становится первым, можно на коммутативность не проверять, то есть для этого операнда мы не будем использовать круглые скобки при равенстве приоритетов.

Screen Shot 2015-03-29 at 10.34.30 PM
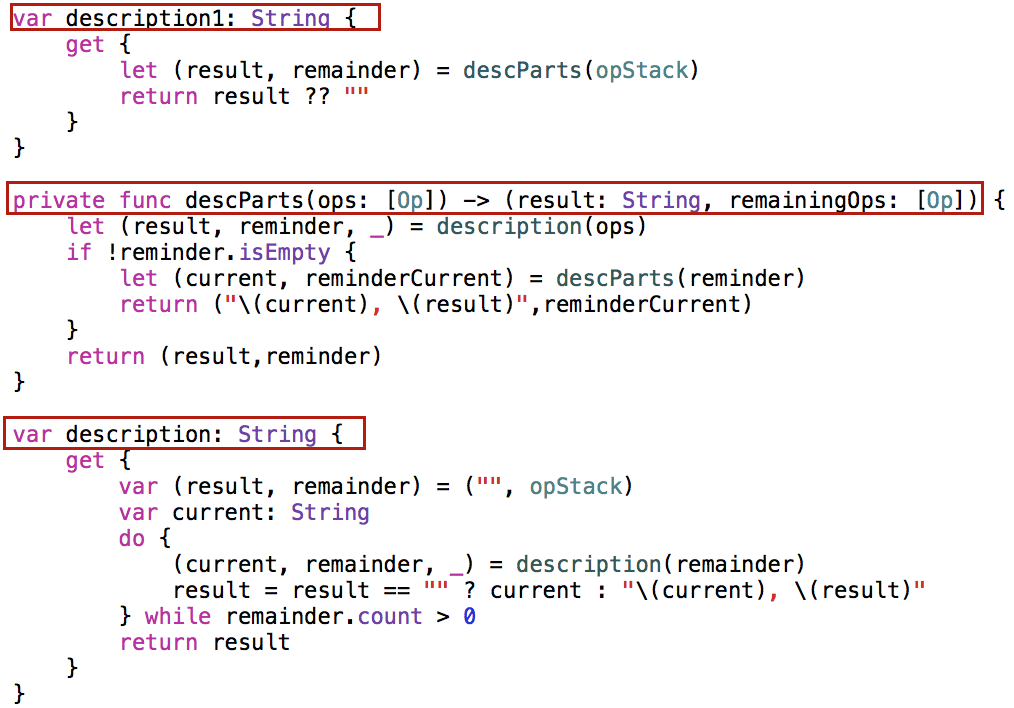
Кроме того, понятно, что на выходе этой рекурсивный функции result будет обычной строкой String, а не  Optional, так как мы нигде не возвращаем nil. Это упростит некоторые выражения. Скорректируются две non-private переменные var description и var description1 и рекурсивный метод более высоко порядка для расчета нескольких законченных выражений descParts (в учебных целях я оставила в коде два варианта создания инфиксного представления нашего стэка: description c применением обычной do…while конструкции и description1 с использованием еще одного  рекурсивный метода).

Screen Shot 2015-03-29 at 12.17.47 PM

Были проведены многочисленные тесты на правильность формирования переменной description. Среди них особенно выделяются те, которые не дают правильный результат, если не учесть «коммутативность» операций.
Стэк 3 ↵ 4 ↵ 5  +  — должен давать 3 — ( 5 + 4), а не 3 — 5 + 4

Стэк 3 ↵ 4 ↵  5  ×  ÷ — должен давать  3 ÷ (5 ×  4), а не 3 ÷ 5 ×  4

Стэк 10 ↵ 5↵  2  — —  — должен давать 10 — (5 — 2), а не 10 — 5 —  2

Стэк 3 ↵ 5↵ — 7 ↵ 8↵ —  —  должен давать 3 − 5 − (7 − 8), а не 3 − 5 − 7 − 8

Screen Shot 2015-08-24 at 8.52.47 AM

Код можно посмотреть на Github.

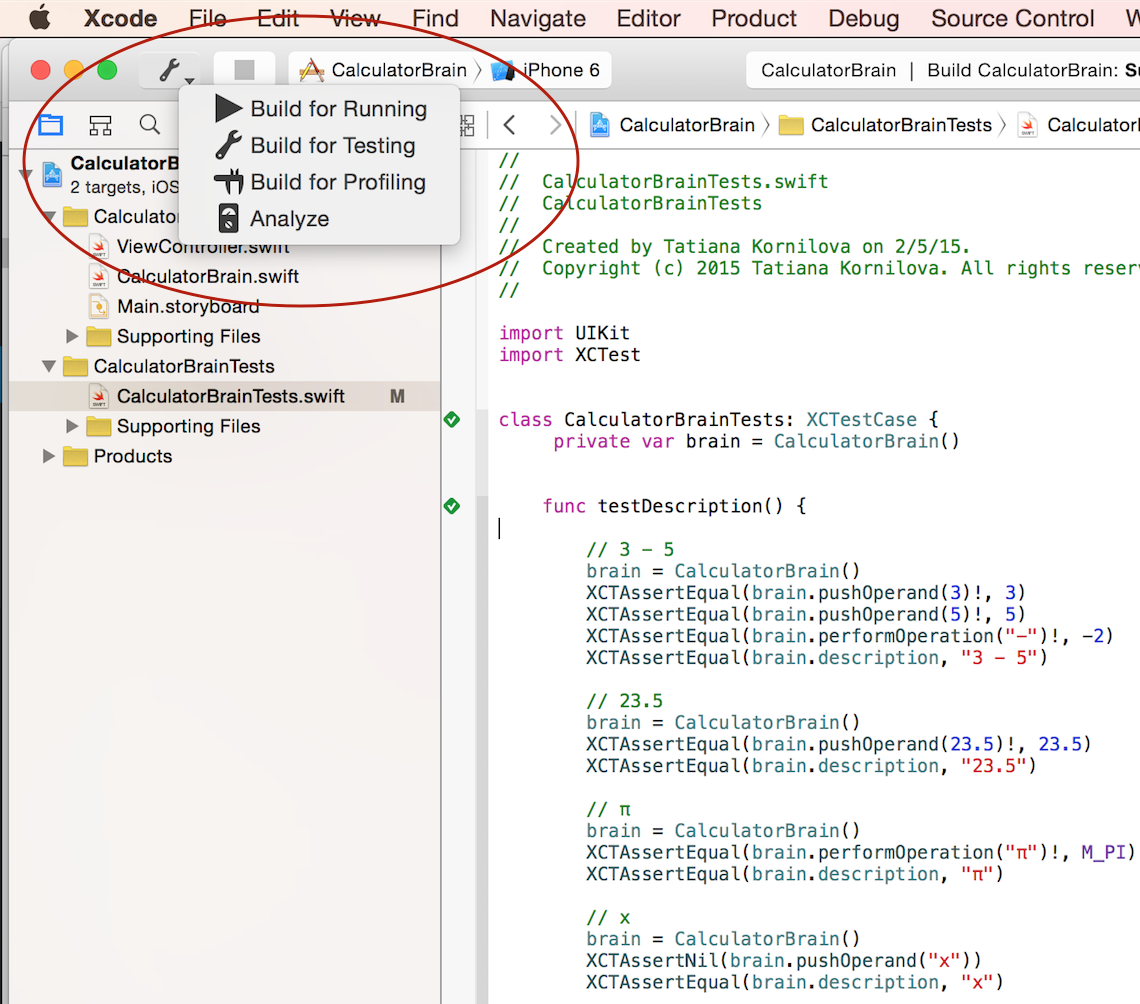
Для тестирования необходимо разместить тесты в файле CalculatorBrainTests и вместо запуска приложения кнопкой Run, нужно использовать Test

Screen Shot 2015-08-24 at 8.57.18 AM

Полный список тестов на правильность формирования description приведен ниже.

[objc]
class CalculatorBrainTests: XCTestCase {
private var brain = CalculatorBrain()

func testPushOperandVariable() {
XCTAssertNil(brain.pushOperand("x"))
brain.setVariable ("x", value: 5.2)
XCTAssertEqual(5.2, brain.pushOperand("x")!)
XCTAssertEqual(10.4, brain.performOperation("+")!)
}

func testDescription() {
// cos(10)
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(10)!, 10)
XCTAssertTrue(brain.performOperation("cos")! — -0.839 < 0.1)
XCTAssertEqual(brain.displayStack(), "10.0 cos")

// 3 — 5
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("−")!, -2)
XCTAssertEqual(brain.description, "3 − 5")

// 23.5
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(23.5)!, 23.5)
XCTAssertEqual(brain.description, "23.5")

// π
brain = CalculatorBrain()
XCTAssertEqual(brain.performOperation("π")!, M_PI)
XCTAssertEqual(brain.description, "π")

// x
brain = CalculatorBrain()
XCTAssertNil(brain.pushOperand("x"))
XCTAssertEqual(brain.description, "x")

// √(10) + 3
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(10)!, 10)
XCTAssertTrue(brain.performOperation("√")! — 3.162 < 0.1)
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertTrue(brain.performOperation("+")! — 6.162 < 0.1)
XCTAssertEqual(brain.description, "√(10) + 3")

// √(3 + 5)
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("+")!, 8)
XCTAssertTrue(brain.performOperation("√")! — 2.828 < 0.1)
XCTAssertEqual(brain.description, "√(3 + 5)")

// 3 + (5 + 4) —> 3 + 5 + 4
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.pushOperand(4)!, 4)
XCTAssertEqual(brain.performOperation("+")!, 9)
XCTAssertEqual(brain.performOperation("+")!, 12)
XCTAssertEqual(brain.description, "3 + 5 + 4")

// (3 + 5) * 6
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("+")!, 8)
XCTAssertEqual(brain.pushOperand(6)!, 6)
XCTAssertEqual(brain.performOperation("×")!, 48)
XCTAssertEqual(brain.description, "(3 + 5) × 6")

// √(3 + √(5)) ÷ 6
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertTrue(brain.performOperation("√")! — 2.236 < 0.1)
XCTAssertTrue(brain.performOperation("+")! — 5.236 < 0.1)
XCTAssertTrue(brain.performOperation("√")! — 2.288 < 0.1)
XCTAssertEqual(brain.pushOperand(6)!, 6)
XCTAssertTrue(brain.performOperation("÷")! — 0.381 < 0.1)
XCTAssertEqual(brain.description, "√(3 + √(5)) ÷ 6")

// ? + 3
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertNil(brain.performOperation("+"))
XCTAssertEqual(brain.description, "? + 3")

// √(3 + 5), cos(π)
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("+")!, 8)
XCTAssertTrue(brain.performOperation("√")! — 2.828 < 0.1)
XCTAssertEqual(brain.performOperation("π")!, M_PI)
XCTAssertEqual(brain.performOperation("cos")!, -1)
XCTAssertEqual(brain.description, "√(3 + 5), cos(π)")

// 3 * (5 + 4)
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.pushOperand(4)!, 4)
XCTAssertEqual(brain.performOperation("+")!, 9)
XCTAssertEqual(brain.performOperation("×")!, 27)
XCTAssertEqual(brain.description, "3 × (5 + 4)")

// 3 — (5 + 4) commutative test
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.pushOperand(4)!, 4)
XCTAssertEqual(brain.performOperation("+")!, 9)
XCTAssertEqual(brain.performOperation("−")!, -6)
XCTAssertEqual(brain.description, "3 − (5 + 4)")

// 3 / (5 × 4) commutative test
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.pushOperand(4)!, 4)
XCTAssertEqual(brain.performOperation("×")!, 20)
XCTAssertEqual(brain.performOperation("÷")!, 0.15)
XCTAssertEqual(brain.description, "3 ÷ (5 × 4)")

// (3 + 5) + (7 + 8)
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("+")!, 8)
XCTAssertEqual(brain.pushOperand(7)!, 7)
XCTAssertEqual(brain.pushOperand(8)!, 8)
XCTAssertEqual(brain.performOperation("+")!, 15)
XCTAssertTrue(brain.performOperation("÷")! — 0.53333 < 0.1)
XCTAssertEqual(brain.description, "(3 + 5) ÷ (7 + 8)")

// 3 — 5 — (7 — 8) commutative test
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("−")!, -2)
XCTAssertEqual(brain.pushOperand(7)!, 7)
XCTAssertEqual(brain.pushOperand(8)!, 8)
XCTAssertEqual(brain.performOperation("−")!, -1)
XCTAssertEqual(brain.performOperation("−")!, -1)
XCTAssertEqual(brain.description, "3 − 5 − (7 − 8)")

// (3 + 5) × (7 + 8)
brain = CalculatorBrain()
XCTAssertEqual(brain.pushOperand(3)!, 3)
XCTAssertEqual(brain.pushOperand(5)!, 5)
XCTAssertEqual(brain.performOperation("+")!, 8)
XCTAssertEqual(brain.pushOperand(7)!, 7)
XCTAssertEqual(brain.pushOperand(8)!, 8)
XCTAssertEqual(brain.performOperation("+")!, 15)
XCTAssertEqual(brain.performOperation("×")!, 120)
XCTAssertTrue(brain.performOperation("√")! — 10.9544 < 0.1)
XCTAssertEqual(brain.description, "√((3 + 5) × (7 + 8))")

}
}

[/objc]

Возможен и немного другой рекурсивный алгоритм description, убирающий лишние круглые скобки с помощью приоритетов и коммутативности. Если мы вернемся к нашему примеру X — (Y+Z), то мы можем проводить  анализ приоритетов как находясь в родительской операции (в нашем случае «-«), так и в операции операнда (в нашем случае «+». В первом случае мы при равенстве приоритетов анализируем коммутативность текущей родительской операции и заключаем в круглые скобки операнды. Во втором случае мы анализируем коммутативность родительской операции, которая должна быть передана на вход description, и в круглые скобки придется заключать весь результат операции операнда.

У нас работает первый вариант этого алгоритма.

В учебных целях привожу второй вариант алгоритма, который в коде на Github закомментирован.

Screen Shot 2015-03-29 at 1.27.50 PM

Для использования этого метода description необходимо в var precedence: Int 
возвращать вместо return Int.max другое  return 0
Но чем интересен этот вариант ? При вызове этого метода  description (remainder) в переменной  var description: String  можно не добавлять дополнительный аргумент, так как будет использоваться значение дополненного аргумент по  умолчанию opPrev: Op = .Variable («x»), которое имеет precedence = 0 и commutative = true. Это демонстрирует гибкие возможности Swift добавлять новые аргументы в функции, не меняя обращения к ним.

Код для Swift 1.2  и iOS 8.4 можно посмотреть на Github.

Код для Swift 2.0  и iOS 9 можно посмотреть на Github.

Продолжение следует…

Задание 2. Решение — Убираем лишние скобки (дополнительный пункт 1) Swift 1.2 и Swift 2.0: 2 комментария

  1. Добрый вечер!
    Поясни пожалуйста что за калдунство происходит когда мы добавляем переменные precedence и commutative в тип Op. Мы добавляем к бинарной операции 2 параметра типа Int и Bool:

    BinaryOperation(String, Int, Bool, (Double, Double ) -> Double)

    Затем присваиваем им значения:

    lernOp(Op.BinaryOperation(«÷», 2, false, {$1 / $0})).

    Мне не понятно каким образом свифт понимает что значения «2» и «false» относятся к precedence и commutative соответсвенно. Сначала я думал что сопоставление происходит по типу передаваемых данных. Я добавил в Op ещё одно свойство типа Int, но свифт по прежнему безошибочно присваивает 2 в precedence.

    Объясни те пожалуйста как это работает, или дайте ссылку где можно изучит этот момент подробнее.

    Спасибо!

    • Никакой магии нет. Потому что есть readonly вычисляемые свойства
      var precedence: Int {
      get {
      switch self {
      case .BinaryOperation(_, let precedence, _, _, _):
      return precedence
      default:
      return Int.max
      }
      }
      }

      var commutative: Bool {
      get {
      switch self {
      case .BinaryOperation(_, _ , let commutative, _, _):
      return commutative
      default:
      return true
      }
      }
      }

      которые для каждой.BinaryOperation(_, _ , let commutative, _, _) возвращают соответственно второе и третье ассоциативные значения.

Обсуждение закрыто.